Интернет предоставляет пользователю более быстрый способ поиска информации в сравнении с традиционными. Поиск информации в 1Щегпе1 может быть произведен по нескольким методам, значительно различающимся как по эффективности и качеству поиска, так и по типу извлекаемой информации. В зависимости от целей и задач ищущего методы поиска информации в 1Щегпе1 используются по отдельности или в комбинации друг с другом.

1. Непосредственное обращение по 1ЖЬ. Простейший метод поиска, который подразумевает наличие адреса и сводится к обращению клиента к серверу определенного типа, т. е. отправки запроса с использованием определенного протокола.

Обычно этот процесс начинается после ввода адреса в соответствующей строке программы браузера или выборе описания адреса в окне просмотра.

При непосредственном обращении по адресу можно использовать сокращенную запись стандарта 1ЖЬ - опускать элементы по умолчанию. Например, опускать название протокола (выбирается протокол по домену нижнего уровня или берется сервис по умолчанию); опускать имя файла по умолчанию (зависит от конфигурации сервера) и последнего символа «/»; опускать имя сервера и использовать относительную адресацию имен каталогов.

Заметим, что этот метод является основой работы более сложных технологий, так как в результате сложных процессов все сводится к непосредственному обращению по адресу 1ЖЬ.

2. Использование набора ссылок. Большинство серверов, представляющие гипертекстовые материалы общего вида, предлагают ссылки и на другие серверы (содержат 1ЖБ-адреса других ресурсов). Такой способ поиска информации называется поиском с помощью наборов ссылок. Поскольку все сайты в пространстве VWV фактически оказываются связанными между собой, поиск информации может быть произведен путем последовательного просмотра связанных страниц с помощью браузера.

Следует заметить, что администраторы сети не ставят себе целью поместить полный набор ссылок по основной тематике своего сервера и постоянно следить за их правильностью, поэтому такой метод поиска не дает полноты и не гарантирует достоверности получения информации. Хотя этот полностью ручной метод поиска выглядит полным анахронизмом в сети, содержащей более 60 млн узлов, «ручной» просмотр УеЬ-страниц часто оказывается единственно возможным на заключительных этапах информационного поиска, когда механическое «копание» уступает место более глубокому анализу. Использование каталогов, классифицированных и тематических списков и всевозможных небольших справочников также относится к этому виду поиска.

3. Использование специализированных поисковых механизмов: поисковых машин, каталогов ресурсов, метапоиск, поиск людей, адресов телеконференции, поиск в файловых архивах и др.

Основная идея поисковых машин (серверов) - создание базы данных из слов, встречающихся в документах МегпеГ в которой при каждом слове будет храниться список документов, содержащих это слово. Поиск осуществляется в содержание документов. Документы, попадающие в ШетеГ регистрируются в поисковых машинах с помощью специальных программ и не требуют участия человека. Исходя из этого, мы получаем полную, но отнюдь не достоверную информацию.

Несмотря на обилие слов и словоформ в естественных языках, большинство из них употребляется нечасто, что было замечено ученым-лингвистом Ципфом еще в конце 40-х гг. XX в. К тому же наиболее употребительные слова - это союзы, предлоги и артикли, т. е слова, совершенно бесполезные при поиске информации. В результате словарь самой крупной поисковой машины 11й:епе1 АЙаУ^а имеет объем всего лишь несколько Гбайт. Поскольку все морфологические единицы в словаре упорядочены, поиск нужного слова может выполняться без последовательного просмотра. Наличие списков документов, в которых встречается искомое слово, позволяет поисковой машине выполнять операции с этими списками: их слияние, пересечение или вычитание.

Запрос поисковой машине может быть двух видов: простой и сложный.

При простом запросе указывается слово или набор слов не отделенных никакими знаками. При сложном запросе слова могут быть отделены друг от друга логическими операторами и их комбинациями. Эти операторы имеют приоритет.

От того, как сформулирован запрос, простой он или сложный, зависит правильность и количество выданных поисковой машиной документов.

Многие поисковые машины используют для поиска тематические каталоги или существуют совместно с ними. Поэтому бывает довольно сложно классифицировать поисковые системы. Большинство из них можно отнести в равной степени как к поисковым машинам, так и к классификационным каталогам.

К числу самых известных поисковых серверов можно отнести следущие: американские (AltaVista, Hot Bot, Lycos, Open Text, Mckinley, Excite, Cuiwww); русские (Yandex, Search, Aport, Tela, Rambler).

В каталогах ресурсов используется иерархическая (древовидная) и/или сетевая модель базы данных, так как любой ресурс, имеющий URL-адрес, описание и другую информацию, подчинен некой классификации - она называется классификатором. Разделы классификатора называются рубриками. Библиотечный аналог каталога - систематический каталог.

Классификатор разрабатывается и совершенствуется коллективом авторов. Затем его использует другой коллектив специалистов, называемых систематизаторами. Систематизаторы, зная классификатор, читают документы и приписывают им классификационные индексы, указывающие, каким разделам классификатора эти документы соответствуют.

Существуют приемы, облегчающие поиск информации с помощью каталогов. Эти приемы носят название отсылка и ссылка и оба они применяются создателями каталогов в Internet. Вышеназванные приемы используются в ситуации, когда документ может быть отнесен к одному из нескольких разделов классификатора, а лицо, осуществляющее поиск, может не знать, к какому именно разделу.

Отсылка используется тогда, когда создатели классификатора и систематизаторы в состоянии принять четкое решение об отнесении документа к одному из разделов классификатора, а пользователь в поисках этого документа может обратиться к другому разделу. Тогда в этом другом разделе помещается отсылка (См.) в тот раздел классификатора, в котором действительно размещена информация о документах данного типа.

Например, информация о картах стран может быть размещена в разделах «Наука-География-Страна», «Экономика-География-Страна», «Справочники-Карта-Страна». Принимается решение, что карты стран помещаются во второй раздел «Экономика-География-Страна», а в остальные два раздела помещаются отсылки в него. Этот прием активно используется в Yahoo!.

Ссылка (См. также) используется в менее однозначной ситуации, когда даже создатели классификатора и систематизаторы не в состоянии принять четкого решения об отнесении документов к определенному разделу классификатора. Особенно она применяется в каталогах, использующих сетевую модель базы данных.

Распространены следующие классификационные каталоги: европейские (Yellow Web, Euroseek); американские (Yahoo!, Magellan, Infoseek и др.); русские (WWW, Stars, Weblist, Rocit, Au).

Преимущество метапоиска перед поисковыми серверами и каталогами в том, что он представляет единый интерфейс или точку доступа к индексам Internet.

Выделяют два вида инструментов множественного доступа:

• 1) службы множественного доступа из своих «начальных страниц» предоставляют меню с выбором поисковых средств. Популярность этих служб объясняется тем, что так много поисковых механизмов представлены в виде меню. Они допускают легкий переход от одного поискового средства к другому, не нужно ни запоминать URL-адреса, ни вводить их с клавиатуры в программу просмотра. Самые популярные службы множественного доступа All-in-One (http://www.allonesearch.com); С/Net (http://www.search, com); Internet Sleuth (http://isleuth.com);
• 2) мета-индексы, часто называемые мульти- или интегрированными поисковыми службами, обеспечивают единую поисковую форму, в которой пользователь вводит поисковый запрос, посы-лаемыи в несколько поисковых механизмов одновременно, и отдельные результаты представляются единым списком. Этот тип службы представляет ценность, в случае если нужна максимальная выборка документов по какому-либо определенному предмету и когда документ уникален.

Еще одним достоинством мета-индекса является то, что результаты поиска каждого поискового механизма достаточно уникальны, т. е мета-индекс не выдает дважды повторяющиеся ссылки.

Главный недостаток этого поискового механизма в том, что он не позволяет использовать индивидуальные свойства различных механизмов поиска.

Самые популярные мета-индексы Beaucoup (http://www.bea coup.com); Следопыт (http://www.medialingua.ru/www/wwwsearc.htm).

Следует заметить, что разделение между этими двумя службами весьма расплывчато. Некоторые более крупные разделы предлагают доступ к отдельным поисковым механизмам, а также ме-та-индексный поиск.

До сих пор был рассмотрен поиск в основном гипертекстовых материалов. Однако с тем же успехом можно искать и другие ресурсы Internet. Для этого существуют как специализированные поисковые механизмы (осуществляющие поиск только однотипных ресурсов), так и «обыкновенные» поисковые механизмы, предлагающие дополнительные возможности поиска не гипертекстовых документов.

Поиск людей. Нет единого списка или каталога адресов электронной почты, так же как нет единого печатного телефонного справочника для всего мира. Существует несколько коммерческих и некоммерческих справочных служб, но большинство их включают в себя какой-либо отдельный регион или дисциплину. Они составляются различными методами и могут быть собраны специальными компьютерными программами из сообщения групп новостей Internet или запущены отдельными лицами, которые необязательно являются владельцами адресов. Эти каталоги часто называются «белыми страницами» и включают в себя каталоги адресов электронной почты и почтовых адресов, а также телефонные номера. Один из самых надежных способов нахождения информации о персональных контактах, если вы знаете организацию, к которой относится человек, - это обратиться к начальной странице организации. Другой способ - использование персональных каталогов.

В результате использования поисковый механизм должен выдать URL-адрес электронной почты (e-mail) нужного человека.

Основные персональные каталоги: Кто Где (http://www. whowhere.com); Народ Яху (http://yahoo.com/search/people); Four 11 (http://www.four 1 l.com).

Специализированных поисковых механизмов, осуществляющих поиск URL-адресов конференций, не так уж и много, в частности, это DejaNews (http://www.dejanews.com -самая изощренная система поиска в телеконференциях (Usenet). Она характеризуется обилием возможностей расширенного поиска, имеет полезные фильтры для «очистки» результата, формально-логический синтаксис запросов и возможность поиска файлов.

Многие поисковые механизмы предоставляют возможность поиска конференций как дополнительную услугу (Yahoo!, Alta Vista, Anzwers, Galaxy, Info Seek и др.). В режим поиска конференций можно войти с помощью кнопки Usenet.

Поиск в файловых архивах. Internet содержит огромное количество ресурсов. Немалую их часть составляют файловые архивы на FTP-серверах. Для их поиска применяются специализированные поисковые механизмы. Регистрация файлов происходит с помощью специальных программ, причем индексируются имена файлов.

Некоторые неспециализированные поисковые механизмы также предоставляют возможность поиска в файловых архивах. Например, введя в AltaVista запрос search.ftp, мы получим ссылки на сервера, специализирующиеся на поиске файлов на FTP-архи-вах. В результате использования поисковый механизм должен выдать U RL-адрес файла.

Основные поисковые механизмы в файловых архивах: Archie (http://archie.de); Filez (http://www.filez.com); FFP-Search (http:// ftpsearch.city.ru).

1. Назначение и классификация методов поисковой оптимизации

В связи со сложностью объектов проектирования критерии качества и ограничения задачи параметрической оптимизации (1.5), как правило, слишком сложны для применения классических методов поиска экстремума. Поэтому на практике предпочтение отдается методам поисковой оптимизации. Рассмотрим основные этапы любого метода поиска.

Исходными данными в методах поиска являются требуемая точность метода и начальная точка поиска Х 0 .

Затем выбирается величина шага поиска h, и по некоторому правилу происходит получение новых точек Х k +1 по предыдущей точке Х k , при k = 0,1,2,… Получение новых точек продолжают до тех пор, пока не будет выполнено условие прекращения поиска. Последняя точка поиска считается решением задачи оптимизации. Все точки поиска составляют траекторию поиска.

Методы поиска могут отличаться друг от друга процедурой выбора величины шага h (шаг может быть одинаковым на всех итерациях метода или рассчитываться на каждой итерации), алгоритмом получения новой точки и условием прекращения поиска.

Для методов, использующих постоянную величину шага, h следует выбирать значительно меньше точности h » Öe). Если при выбранной величине шага h не удается получить решение с требуемой точностью, то нужно уменьшить величину шага и продолжить поиск из последней точки имеющейся траектории.

В качестве условий прекращения поиска принято использовать следующие:

все соседние точки поиска хуже, чем предыдущая;

çФ(X k +1) - Ф(X k)ç£ e, то есть значения целевой функции Ф(Х) в соседних точках (новой и предыдущей) отличаются друг от друга на величину не больше, чем требуемая точность e;

то есть все частные производные в новой точке поиска практически равны 0 или отличаются от 0 на величину, не превышающую заданной точности e.

Алгоритм получения новой точки поиска Х k +1 по предыдущей точке Х k свой для каждого из методов поиска, но всякая новая точка поиска должна быть не хуже предыдущей: если задача оптимизации является задачей поиска минимума, то Ф(Х k +1) £ Ф(Х k).

Методы поисковой оптимизации принято классифицировать по порядку производной целевой функции, используемой для получения новых точек. Так, в методах поиска нулевого порядка не требуется вычисления производных, а достаточно самой функции Ф(Х). Методы поиска первого порядка используют первые частные производные, а методы второго порядка используют матрицу вторых производных (матрицу Гессе).

Чем выше порядок производных, тем более обоснованным является выбор новой точки поиска и тем меньше число итераций метода. Но при этом возрастает трудоемкость каждой итерации из-за необходимости численного расчета производных.

Эффективность поискового метода определяют по числу итераций и по количеству вычислений целевой функции Ф(Х) на каждой итерации метода (N). Рассмотрим наиболее распространенные методы поиска, расположив их в порядке уменьшения числа итераций.

Для методов поиска нулевого порядка справедливо следующее: в методе случайного поиска нельзя заранее предсказать количество вычислений Ф(Х) на одной итерации N, а в методе покоординатного спуска N £ 2×n, где n- количество управляемых параметров X = (x1, x2.,…,xn).

Для методов поиска первого порядка справедливы следующие оценки: в градиентном методе с постоянным шагом N=2×n; в градиентном методе с дроблением шага N = 2×n + n 1 , где n 1 – число вычислений Ф(Х), необходимых для проверки условия дробления шага; в методе наискорейшего спуска N=2×n+n 2 , где n 2 – число вычислений Ф(Х), необходимых для расчета оптимальной величины шага; а в методе Давидона – Флетчера - Пауэлла (ДФП) N = 2× n + n 3 , где n 3 – число вычислений Ф(Х), необходимых для расчета матрицы, приближающей матрицу Гессе (для величин n 1 , n 2 , n 3 справедливо соотношение n 1 < n 2 << n 3).

И, наконец, в методе второго порядка - методе Ньютона N = 3×n 2 . При получении данных оценок предполагается приближенное вычисление производных по формулам конечных разностей / 6 /:

то есть для вычисления производной первого порядка нужно знать два значения целевой функции Ф(Х) в соседних точках, а для второй производной – значения функции в трех точках.

На практике широкое применение нашли метод наискорейшего спуска и метод ДФП, как методы с оптимальным соотношением числа итераций и их трудоемкости.

2. Методы поиска нулевого порядка

2.1. Метод случайного поиска

В методе случайного поиска исходными данными являются требуемая точность метода e, начальная точка поиска Х 0 = (x1 0 , x2. 0 ,…,xn 0) и величина шага поиска h. Поиск новых точек производится в случайном направлении, на котором и откладывается заданный шаг h (рис. 2.1), таким образом получают пробную точку Х ^ и проверяют, является ли пробная точка лучшей, чем предыдущая точка поиска. Для задачи поиска минимума это означает, что

Ф(Х ^) £ Ф(Х k) , k = 0,1,2… (2.4)

Если условие (2.4) выполнено, то пробную точку включают в траекторию поиска Х k +1 = Х ^ . В противном случае, пробную точку исключают из рассмотрения и производят выбор нового случайного направления из точки Х k , k = 0,1,2,.

Несмотря на простоту данного метода, его главным недостатком является тот факт, что заранее неизвестно, сколько случайных направлений потребуется для получения новой точки траектории поиска Х k +1 , что делает затраты на проведение одной итерации слишком большими. Кроме того, поскольку при выборе направления поиска не используется информация о целевой функции Ф(Х), число итераций в методе случайного поиска очень велико.

В связи с этим метод случайного поиска используется для исследования малоизученных объектов проектирования и для выхода из зоны притяжения локального минимума при поиске глобального экстремума целевой функции /6/.

2.2. Метод покоординатного спуска

В отличие от метода случайного поиска, в методе покоординатного спуска в качестве возможных направлений поиска выбирают направления, параллельные осям координат, причем движение возможно как в сторону увеличения, так и уменьшения значения координаты.

Исходными данными в методе покоординатного спуска являются величина шага h и начальная точка поиска Х 0 = (x1 0 , x2. 0 ,…,xn 0). Движение начинаем из точки Х 0 вдоль оси x1 в сторону увеличения координаты. Получим пробную точку Х ^ с координатами (x1 0 +h, x2 0 ,…,xn 0), при k = 0.

Сравним значение функции Ф(Х ^) с значением функции в предыдущей точке поиска Х k . Если Ф(Х ^) £ Ф(Х k) (мы предполагаем, что требуется решить задачу минимизации целевой функции Ф(Х)), то пробную точку включают в траекторию поиска (Х k +1 = Х ^).

В противном случае, пробную точку исключаем из рассмотрения и получаем новую пробную точку, двигаясь вдоль оси x1 в сторону уменьшения координаты. Получим пробную точку Х ^ = (x1 k -h, x2. k ,…,xn k). Проверяем, если Ф(Х ^) > Ф(Х k), то продолжаем движение вдоль оси x 2 в сторону увеличения координаты. Получим пробную точку Х ^ = (x1 k , x2. k +h,…,xn k) и т.д. При построении траектории поиска повторное движение по точкам, вошедшим в траекторию поиска, запрещено. Получение новых точек в методе покоординатного спуска продолжается до тех пор, пока не будет получена точка Х k , для которой все соседние 2×n пробных точек (по всем направлениям x1, x2.,…,xn в сторону увеличения и уменьшения значения каждой координаты) будут хуже, то есть Ф(Х ^) > Ф(Х k). Тогда поиск прекращается и в качестве точки минимума выбирается последняя точка траектории поиска Х* = Х k .

3. Методы поиска первого порядка

3.1. Структура градиентного метода поиска

В методах поиска первого порядка в качестве направления поиска максимума целевой функции Ф(Х) выбирается вектор градиент целевой функции grad (Ф(Х k)), для поиска минимума – вектор антиградиент -grad (Ф(Х k)). При этом используется свойство вектора градиента указывать направление наискорейшего изменения функции:

Для изучения методов поиска первого порядка важно также следующее свойство: вектор градиент grad (Ф(Х k)) направлен по нормали к линии уровня функции Ф(Х) в точке Х k (см. рис. 2.4). Линии уровня – это кривые, на которых функция принимает постоянное значение (Ф(Х) = соnst).

В данной главе мы рассмотрим 5 модификаций градиентного метода:

градиентный метод с постоянным шагом,

градиентный метод с дроблением шага,

метод наискорейшего спуска,

метод Давидона-Флетчера-Пауэлла,

двухуровневый адаптивный метод.

3.2. Градиентный метод с постоянным шагом

В градиентном методе с постоянным шагом исходными данными являются требуемая точность e, начальная точка поиска Х 0 и шаг поиска h.

Получение новых точек производится по формуле.

Поисковая оптимизация – это комплекс мер для повышения позиций сайтов или отдельных их веб-страниц в выдаче поисковых систем.

Основными инструментами поисковой оптимизации являются:

программирование,

маркетинг,

специальные методы работы с контентом.

Чаще всего, более высокая позиция сайта в результатах поиска приводит больше заинтересованных пользователей на сайт. При анализе эффективности поисковой оптимизации определяется стоимость целевого посетителя с учетом времени вывода сайта на указанные позиции, а также учитывается количество пользователей, которые задержатся на сайте и произведут какие-либо действия.

Суть поисковой оптимизации заключается в создании страниц, содержимое которых удобно как для чтения как пользователем, так и для индексирования поисковыми роботами. Оптимизированные страницы поисковая система вносит в свою БД таким образом, что при запросе пользователя по ключевым словам сайт размещается в верхней части результатов поиска, т.к. вероятность посещения сайта пользователем возрастает. Следовательно наоборот, если оптимизация не проводилась, то рейтинг сайта в результат поиска будет низким (далеко не на первой странице), и вероятность, что пользователь зайдет на такой сайт минимальна.

Не редки случаи, когда роботы поисковых машин не в состоянии считать веб-страницу. Такой сайт вообще не попадает в результаты поисковой выдачи, и вероятность, что посетители найдут его вообще стремиться к нулю.

Главная цель поисковой оптимизации сайта заключается в повышении позиций сайта в результатах поисковых систем. Для этого следует проанализировать существующие методы оптимизации и выявить среди них наиболее эффективные.

Методы поисковой оптимизации разработаны с учетом основных принципов работы информационно-поисковых систем. Следовательно, прежде всего необходимо оценить параметры сайта, по которым поисковые системы вычисляют его релевантность, а именно:

плотность ключевых слов (современные алгоритмы поисковых систем производят анализ текста и отсеивают страницы, в которых ключевые слова встречаются слишком часто),

индекс цитирования сайта (кстати, в сети предлагается множество инструментов для повышения цитируемости сайта, т.е. попросту можно купить тиц), который зависит от авторитетности и количества веб-ресурсов, которые ссылаются на сайт,

организация ссылок с сайтов, тематика которых идентична тематике оптимизируемого сайта.

Таким образом, все факторы, которые влияют на положение сайта в странице результатов поиска системы, можно разбить на внутренние и внешние. Соответственно, оптимизация требует работы как с внешними факторами, так и с внутренними: приведение текста на страницах в соответствие с ключевыми запросами; улучшение количества и качества контента на сайте; стилистическое оформление текста и т.п..

Методы поисковой оптимизации. Большинство специалистов используют поисковую оптимизацию без применения недобросовестных и запрещённых методов, что подразумевает комплекс мер для повышения посещаемости веб-сайта, который основывается на анализе поведения целевых посетителей.

Исследование, проведенное в работе позволило выделить наиболее эффективные приемы поисковой оптимизации:

повышение видимости сайта роботами поисковых систем;

улучшение удобства сайта для посетителей;

совершенствование контента на сайте;

анализ запросов, связанных с продвигаемым сайтом и его рубриками;

поиск сайтов родственной тематики для создания партнёрских программ и обмена ссылок.

Проведен анализ наиболее распространенных методов внутренней поисковой оптимизации, таких как:

подбор и размещение в коде сайта мета-тегов, содержащих краткое описание контента сайта; этот метод позволяет выделить ключевые слова и словосочетания, по которым оптимизируемый сайт должен находиться поисковыми системами,

использование «понятных URL», что делает сайт удобным не только для пользователей, но и для поисковых машин, которые учтут тему страницы,

оптимизация текстов на сайте, что есть обеспечение соответствия текстов мета-тегам. В тексте должны встречаться слова, обозначенные в мета-тегах как ключевые. При этом не стоит забывать, что переизбыток ключевиков в тексте может и навредить. Прежде всего, текст может стать просто нечитаемым. Кроме того, поисковые системы могут расценивать это как спам. Возможно также увеличение «веса» слова в тексте за счёт использования элементов форматирования.

В связи со сложностью и малой изученностью объектов проектирования и критерии качества, и ограничения задачи параметрической оптимизации, как правило, слишком сложны для применения классических методов поиска экстремума. Поэтому на практике предпочтение отдается методам поисковой оптимизации. Рассмотрим основные этапы любого метода поиска.

Исходными данными в методах поиска являются требуемая точность метода e и начальная точка поиска Х 0 .

Затем выбирается величина шага поиска h , и по некоторому правилу происходит получение новых точек Х k +1 по предыдущей точке Х k при k = 0, 1, 2, … Получение новых точек продолжают до тех пор, пока не будет выполнено условие прекращения поиска. Последняя точка поиска считается решением задачи оптимизации. Все точки поиска составляют траекторию поиска.

Методы поиска отличаются друг от друга процедурой выбора величины шага h (шаг может быть одинаковым на всех итерациях метода или рассчитываться на каждой итерации), алгоритмом получения новой точки и условием прекращения поиска.

Для методов, использующих постоянную величину шага, h следует выбирать значительно меньше точности e . Если при выбранной величине шага h не удается получить решение с требуемой точностью, то нужно уменьшить величину шага и продолжить поиск из последней точки имеющейся траектории.

В качестве условий прекращения поиска принято использовать следующие:

1) все соседние точки поиска хуже, чем предыдущая;

2) çФ(X k +1 )–Ф(X k ) ç £ e , то есть значения целевой функции Ф(Х) в соседних точках (новой и предыдущей) отличаются друг от друга на величину не больше, чем требуемая точность e ;

3) ,i = 1, …, n, то есть все частные производные в новой точке поиска практически равны 0, то есть отличаются от 0 на величину, не превышающую точности e.

Алгоритм получения новой точки поиска Х k +1 по предыдущей точке Х k свой для каждого из методов поиска, но всякая новая точка поиска должна быть не хуже предыдущей: если задача оптимизации является задачей поиска минимума, то Ф(Х k +1 ) £ Ф(Х k ).

Методы поисковой оптимизации принято классифицировать по порядку производной целевой функции, используемой для получения новых точек. Так, в методах поиска нулевого порядка не требуется вычисления производных, а достаточно самой функции Ф(Х). Методы поиска первого порядка используют первые частные производные, а методы второго порядка используют матрицу вторых производных (матрицу Гессе).

Чем выше порядок производных, тем более обоснованным является выбор новой точки поиска и тем меньше число итераций метода. Но при этом трудоемкость каждой итерации из-за необходимости численного расчета производных.

Эффективность поискового метода определяют по числу итераций и по количеству вычислений целевой функции Ф(Х) на каждой итерации метода.

Рассмотрим наиболее распространенные методы поиска , расположив их в порядке уменьшения числа итераций.

Для методов поиска нулевого порядка справедливо следующее: в методе случайного поиска нельзя заранее предсказать количество вычислений Ф(Х) на одной итерации N , а в методе покоординатного спуска N £ 2×n , где n - количество управляемых параметров X = (x 1 , x 2 .,…, x n ).

Для методов поиска первого порядка справедливы следующие оценки: в градиентном методе с постоянным шагом N = 2 × n ; в градиентном методе с дроблением шага N =2 × n + n 1 , где n 1 – число вычислений Ф(Х), необходимых для проверки условия дробления шага; в методе наискорейшего спуска N = 2 × n + n 2 , где n 2 – число вычислений Ф(Х), необходимых для расчета оптимальной величины шага; а в методе Давидона - Флетчера - Пауэлла (ДФП) N = 2 × n + n 3 , где n 3 – число вычислений Ф(Х), необходимых для расчета матрицы, приближающей матрицу Гессе (для величин n 1 , n 2 , n 3 справедливо соотношение n 1 < n 2 < n 3 ).

И, наконец, в методе второго порядка - методе Ньютона N = 3 × n 2 .

При получении данных оценок предполагается приближенное вычисление производных по формулам конечных разностей, то есть для вычисления производной первого порядка нужно два значения целевой функции Ф(Х), а для второй производной – значения функции в трех точках.

На практике широкое применение нашли метод наискорейшего спуска и метод ДФП, как методы с оптимальным соотношением числа итераций и их трудоемкости.

Начнём рассмотрение методов поиска нулевого порядка. В методе случайного поиска исходными данными являются требуемая точность метода e, начальная точка поиска Х 0 = (x 1 0 , x 2 0 , …, x n 0 ) и величина шага поиска h .

Поиск новых точек производится в случайном направлении, на котором и откладывается заданный шаг h , таким образом получают пробную точку и проверяют, является ли пробная точка лучшей, чем предыдущая точка поиска. Для задачи поиска минимума это означает, что:

(6.19)

Если данное условие выполнено, то пробную точку включают в траекторию поиска (
). В противном случае, пробную точку исключают из рассмотрения и производят выбор нового случайного направления из точки Х k , k = 0, 1, 2, … (рис. 6.3).

Х k +1

Ф(Х)

Несмотря на простоту данного метода, его главным недостатком является тот факт, что заранее неизвестно, сколько случайных направлений потребуется для получения новой точки траектории поиска Х k +1 , что делает затраты на проведение одной итерации слишком большими.

Рис. 6.3. К методу случайного поиска

Кроме того, поскольку при выборе направления поиска не используется информация о целевой функции Ф(Х) , число итераций в методе случайного поиска очень велико.

В связи с этим метод случайного поиска используется для исследования малоизученных объектов проектирования и для выхода из зоны притяжения локального минимума при поиске глобального экстремума целевой функции.

В отличие от метода случайного поиска, в методе покоординатного спуска в качестве возможных направлений поиска выбирают направления, параллельные осям координат, причем движение возможно как в сторону увеличения, так и уменьшения значения координаты.

Исходными данными в методе покоординатного спуска являются величина шага h и начальная точка поиска Х 0 = (x 1 0 , x 2 . 0 ,…, x n 0 ) . Движение начинаем из точки Х 0 вдоль оси x 1 в сторону увеличения координаты. Получим пробную точку
(x 1 k + h , x 2 k ,…, x n k ), k = 0. Сравним значение функции Ф(Х) с значением функции в предыдущей точке поиска Х k .

Если
(мы предполагаем, что требуется решить задачу минимизацииФ(Х) , то пробную точку включают в траекторию поиска (
) .

В противном случае, пробную точку исключаем из рассмотрения и получаем новую пробную точку, двигаясь вдоль оси x 1 в сторону уменьшения координаты. Получим пробную точку
(x 1 k – h , x 2 k ,…, x n k ). Проверяем, если
, то продолжаем движение вдоль осиx 2 в сторону увеличения координаты. Получим пробную точку
(x 1 k + h , x 2 k ,…, x n k ), и т.д.

При построении траектории поиска повторное движение по точкам, вошедшим в траекторию поиска, запрещено.

Получение новых точек в методе покоординатного спуска продолжается до тех пор, пока не будет получена точка Х k , для которой все соседние 2×n пробных точек (по всем направлениям x 1 , x 2 , …, x n в сторону увеличения и уменьшения значения координаты) будут хуже, то есть
. Тогда поиск прекращается и в качестве точки минимума выбирается последняя точка траектории поискаХ*= Х k .

Рассмотрим работу метода покоординатного спуска на примере (рис. 2.21): n = 2, X = (x 1 , x 2 ), Ф(x 1 , x 2 )  min , Ф(x 1 , x 2 ) = (x 1 – 1) 2 + (x 2 – 2) 2 , h = 1, Х 0 = (0, 1) .

Начинаем движение вдоль оси x 1 в сторону увеличения

координаты. Получим первую пробную точку

(x 1 0 + h , x 2 0 ) = (1, 1), Ф () = (1-1) 2 + (1-2) 2 = 1,

Ф(Х 0 ) = (0-1) 2 + (1-2) 2 = 2,

Ф() < Ф(Х 0 )  Х 1 = (1, 1).

x 1 от точки Х 1

=(x 1 1 + h , x 2 1 ) = (2, 1), Ф() = (2-1) 2 + (1-2) 2 = 2,

Ф(Х 1 ) = (1-1) 2 + (1-2) 2 = 1,

то есть Ф() > Ф(Х 1 ) – пробная точка с координатами (2, 1) исключается из рассмотрения, а поиск минимума продолжается из точки Х 1 .

Продолжаем движение вдоль оси x 2 от точки Х 1 в сторону увеличения координаты. Получим пробную точку

= (x 1 1 , x 2 1 + h ) = (1, 2), Ф() = (1-1) 2 + (2-2) 2 = 0,

Ф(Х 1 ) = (1-1) 2 + (1-2) 2 = 1,

Ф() < Ф(Х 1 )  Х 2 = (1, 2).

Продолжаем движение вдоль оси x 2 от точки Х 2 в сторону увеличения координаты. Получим пробную точку

= (x 1 2 , x 2 2 + h ) = (1, 3), Ф() = (1-1) 2 + (3-2) 2 = 1,

Ф(Х 2 ) = (1-1) 2 + (2-2) 2 = 0,

то есть Ф() > Ф(Х 2 ) – пробная точка с координатами (1, 3) исключается из рассмотрения, а поиск минимума продолжается из точки Х 2 .

5. Продолжаем движение вдоль оси x 1 от точки Х 2 в сторону увеличения координаты. Получим пробную точку

= (x 1 2 + h , x 2 2 ) = (2, 2), Ф() = (2-1) 2 + (2-2) 2 =1,

Ф(Х 2 ) = (1-1) 2 + (2 - 2) 2 = 0,

то есть Ф(Х ^ ) > Ф(Х 2 ) – пробная точка с координатами (2, 2) исключается из рассмотрения, а поиск минимума продолжается из точки Х 2 .

6. Продолжаем движение вдоль оси x 1 от точки Х 2 в сторону уменьшения координаты. Получим пробную точку

= (x 1 2 - h , x 2 2 ) = (0, 2), Ф() = (0-1) 2 +(2-2) 2 = 1,

Ф(Х 2 ) = (1-1) 2 + (2 - 2) 2 = 0,

то есть Ф() > Ф(Х 2 ) – пробная точка с координатами (0, 2) исключается из рассмотрения, а поиск минимума закончен, так как для точки Х 2 выполнено условие прекращения поиска. Точкой минимума функции Ф(x 1 , x 2 ) = (x 1 – 1) 2 + (x 2 – 2) 2 является Х * = Х 2 .

В методах поиска первого порядка в качестве направления поиска максимума целевой функции Ф(Х) выбирается вектор градиент целевой функции grad (Ф(Х k )) , для поиска минимума – вектор антиградиент - grad (Ф(Х k )) . При этом используется свойство вектора градиента указывать направление наискорейшего изменения функции:

.

Для изучения методов поиска первого порядка важно также следующее свойство: вектор градиент grad (Ф(Х k )) , направлен по нормали к линии уровня функции Ф(Х) в точке Х k .

Линии уровня – это кривые, на которых функция принимает постоянное значение (Ф(Х) = со nst ).

В данном разделе рассматриваются пять модификаций градиентного метода:

– градиентный метод с постоянным шагом,

– градиентный метод с дроблением шага,

– метод наискорейшего спуска,

– метод Давидона-Флетчера-Пауэлла (ДФП),

– двухуровневый адаптивный метод.

В градиентном методе с постоянным шагом исходными данными являются требуемая точность e , начальная точка поиска Х 0 и шаг поиска h .

Х k+1 = Х k – h × grad Ф (Х k ), k=0,1,2,… (6.20)

Формула (2.58) применяется, если для функции Ф(Х) необходимо найти минимум. Если же задача параметрической оптимизации ставится как задача поиска максимума, то для получения новых точек в градиентном методе с постоянным шагом используется формула:

Х k+1 = Х k + h × grad Ф (Х k ), k = 0, 1, 2, … (6.21)

Каждая из формул (6.20), (6.21) является векторным соотношением, включающим n уравнений. Например, с учетом Х k +1 = (x 1 k +1 , x 2 k +1 ,…, x n k +1 ), Х k =(x 1 k , x 2 k ,…, x n k ) :

(6.22)

или, в скалярном виде,

(6.23)

В общем виде (2.61) можно записать:

(6.24)

В качестве условия прекращения поиска во всех градиентных методах используется, как правило, комбинация двух условий: çФ(X k +1 ) - Ф(X k ) ç £ e или
для всехi =1, …, n .

Рассмотрим пример поиска минимума градиентным методом с постоянным шагом для той же функции, что и в методе покоординатного спуска:

n = 2, X = (x 1 , x 2 ),  =0.1,

Ф(x 1 , x 2 ) = (x 1 – 1) 2 + (x 2 – 2) 2  min , h = 0,3, Х 0 = (0, 1).

Получим точку Х 1 по формуле (2.45):

Ф(X 1 ) = (0.6–1) 2 + (1.6–2) 2 = 0.32, Ф(X 0 ) = (0 –1) 2 + (1–2) 2 = 2.

 Ф(X 1 ) - Ф(X 0 ) =1,68 >  = 0,1  продолжаем поиск.

Получим точку Х 2 по формуле (2.45):

Ф(X 2 ) = (0.84–1) 2 + (1.84–2) 2 = 0.05,

Ф(X 1 ) = (0,6 –1) 2 + (1,6–2) 2 = 0,32.

 Ф(X 1 ) - Ф(X 0 ) =0,27 >  = 0,1  продолжаем поиск.

Аналогично получим X 3:

Ф(X 3 ) = (0.94–1) 2 + (1.94–2) 2 = 0.007,

Ф(X 3 ) = (0,84 –1) 2 + (1,84–2) 2 = 0,05.

Так как условие прекращения поиска выполнено, найдено Х * = X 3 = (0.94, 1.94) с точностью  = 0.1.

Траектория поиска для данного примера приведена на рис. 6.5.

Несомненным преимуществом градиентных методов является отсутствие лишних затрат на получение пробных точек, что снижает затраты на проведение одной итерации. Кроме того, за счет использования эффективного направления поиска (вектора градиента) заметно сокращается и число итераций по сравнению с методом покоординатного спуска.

В градиентном методе можно несколько сократить число итераций, если научиться избегать ситуаций, когда несколько шагов поиска выполняются в одном и том же направлении.

В градиентном методе с дроблением шага процедура подбора величины шага на каждой итерации реализуется следующим образом.

e , начальная точка поиска Х 0 h (обычно h = 1). Получение новых точек производится по формуле:

Х k+1 = Х k – h k × grad Ф (Х k ), k=0,1,2,…, (6.25)

где h k – величина шага на k -ой итерации поиска, при h k должно выполняться условие:

Ф(Х k – h k × grad Ф(Х k )) £ Ф(Х k ) - e× h k ×½ grad Ф(Х k ) ½ 2 . (6.26)

Если величина h k такова, что неравенство (2.64) не выполнено, то производится дробление шага до тех пор, пока данное условие не будет выполнено.

Дробление шага выполняется по формуле h k = h k ×a , где 0 < a < 1.Такой подход позволяет сократить число итераций, но затраты на проведение одной итерации при этом несколько возрастают.

Это обеспечивает простоту замены и дополнения процедур, данных и знаний.

В методе наискорейшего спуска на каждой итерации градиентного метода выбирается оптимальный шаг в направлении градиента.

Исходными данными являются требуемая точность e , начальная точка поиска Х 0 .

Получение новых точек производится по формуле:

Х k+1 = Х k – h k × grad Ф (Х k ), k=0,1,2,… , (6.27)

где h k = arg min Ф(Х k – h k × grad Ф(Х k )) , то есть выбор шага производится по результатам одномерной оптимизации по параметру h (при 0 < h < ¥).

Основная идея метода наискорейшего спуска заключается в том, что на каждой итерации метода выбирается максимально возможная величина шага в направлении наискорейшего убывания целевой функции, то есть в направлении вектора-антиградиента функции Ф(Х) в точке Х k . (рис. 2.23).

При выборе оптимальной величины шага необходимо из множества Х М = {Х ½ Х= Х k – h × grad Ф(Х k ), h Î / h = 22(2h -1)2=8(2h -1)=0.

Следовательно, h 1 = 1/2 – оптимальный шаг на первой итерации метода наискорейшего спуска. Тогда

Х 1 = Х 0 – 1/2grad Ф(Х 0 ),

x 1 1 =0 -1/2 = 1, x 2 1 = 1-1/2 = 2  Х 1 = (1, 2).

Проверим выполнение условий прекращения поиска в точке поиска Х 1 = (1, 2). Первое условие не выполнено

Ф(X 1 )-Ф(X 0 ) = 0-2 =2 >  = 0.1, но справедливо

то есть все частные производные с точностью  можно считать равными нулю, точка минимума найдена: Х*=Х 1 =(1, 2). Траектория поиска приведена на рис. 6.7.

Таким образом, метод наискорейшего спуска нашел точку минимума целевой функции за одну итерацию (из-за того, что линии уровня функции Ф(x 1 , x 2 ) = (x 1 – 1) 2 + (x 2 – 2) 2 . ((x 1 – 1) 2 + (x 2 –2) 2 = const – уравнение окружности, и вектор антиградиент из любой точки точно направлен в точку минимума – центр окружности).

На практике целевые функции гораздо более сложные, линии также имеют сложную конфигурацию, но в любом случае справедливо следующее: из всех градиентных методов в методе наискорейшего спуска наименьшее число итераций, но некоторую проблему представляет поиск оптимального шага численными методами, так как в реальных задачах, возникающих при проектировании РЭС применение классических методов нахождения экстремума практически невозможно.

Для задач оптимизации в условиях неопределенности (оптимизация стохастических объектов), в которых один или несколько управляемых параметров являются случайными величинами, используется двухуровневый адаптивный метод поисковой оптимизации, являющийся модификацией градиентного метода.

Х 0 и начальная величина шага поиска h (обычно
). Получение новых точек производится по формуле:

Х k+1 = Х k – h k+1 × grad Ф(Х k), k = 0,1,2,…, (6.28)

где шаг h k +1 может быть рассчитан по одной из двух формул: h k +1 = h k + l k +1 ×a k , или h k +1 = h k × exp (l k +1 ×a k ) . В качестве понижающего коэффициента выбирают обычно l k =1/ k , где k – номер итерации поискового метода.

Смысл применения коэффициента l k заключается в том, что на каждой итерации производится некоторая корректировка величины шага, при этом чем больше номер итерации метода поиска, тем ближе очередная точка поиска к точке экстремума и тем аккуратнее (меньше) должна быть корректировка шага с тем, чтобы не допустить удаления от точки экстремума.

Величина a k определяет знак такой корректировки (при a k >0 шаг увеличивается, а при a k <0 уменьшается):

a k =sign{(grad Ф (Х k ),grad Ф (Х ))} ,

то есть a k – это знак скалярного произведения векторов градиентов целевой функции в точках Х k и , где=Х k – h k × grad Ф(Х k ) пробная точка, а h k – это шаг, который был использован для получения точки Х k на предыдущей итерации метода.

Знак скалярного произведения двух векторов позволяет оценить величину угла между данными векторами (обозначим этот угол  ). Если   9, то скалярное произведение должно быть положительным, в противном случае – отрицательным. С учетом вышеизложенного нетрудно понять принцип корректировки величины шага в двухуровневом адаптивном методе. Если угол между антиградиентами    (острый угол), то направление поиска из точки Х k выбрано правильно, и величину шага можно увеличить (рис. 6.8).

Рис. 6.8. Выбор направления поиска при   

Если же угол между антиградиентами    (тупой угол), то направление поиска из точки Х k удаляет нас от точки минимума Х* , и шаг нужно уменьшить (рис. 6.9).

Рис. 6.9. Выбор направления поиска при  > 

Метод носит название двухуровневого, так как на каждой итерации поиска анализируются не одна, а две точки и строятся два вектора антиградиента.

Это, конечно, увеличивает затраты на проведение одной итерации, но позволяет проводить адаптацию (настройку) величины шага h k +1 на поведение случайных факторов.

Несмотря на простоту реализации метод наискорейшего спуска не рекомендуется в качестве “серьезной” оптимизационной процедуры для решения задачи безусловной оптимизации функции многих переменных, так как для практического применения он работает слишком медленно.

Причиной этого является тот факт, что свойство наискорейшего спуска является локальным свойством, поэтому необходимо частое изменение направления поиска, что может привести к неэффективной вычислительной процедуре.

Более точный и эффективный метод решения задачи параметрической оптимизации можно получить, используя вторые производные целевой функции (методы второго порядка). Они базируются на аппроксимации (то есть приближенной замене) функции Ф(Х) функцией j (Х) ,

j (Х) = Ф(Х 0 ) + (Х - Х 0 ) т × grad Ф(Х 0 ) + ½ G (X 0 ) × (Х - Х 0 ) , (6.29)

где G (X 0 ) - матрица Гессе (гессиан, матрица вторых производных), вычисленная в точке Х 0 :

¶ 2 Ф(Х) ¶ 2 Ф(Х) . . . ¶ 2 Ф(Х)

¶ x 1 2 ¶ x 1 ¶ x 2 ¶ x 1 ¶ x n

G (X ) = ¶ 2 Ф(Х) ¶ 2 Ф(Х) . . . ¶ 2 Ф(Х)

¶ x 2 ¶ x 1 ¶ x 2 2 ¶ x 2 ¶ x n

¶ 2 Ф(Х) ¶ 2 Ф(Х) . . . ¶ 2 Ф(Х)

¶ x n ¶ x 1 ¶ x n ¶ x 2 ¶ x n 2 .

Формула (2.67) представляет собой первые три члена разложения функции Ф(Х) в ряд Тейлора в окрестности точки Х 0 , поэтому при аппроксимации функции Ф(Х) функцией j (Х) возникает ошибка не более чем ½½Х-Х 0 ½½ 3 .

С учетом (2.67) в методе Ньютона исходными данными являются требуемая точность e , начальная точка поиска Х 0 и получение новых точек производится по формуле:

Х k +1 = Х k – G -1 (Х k ) × grad Ф(Х k), k =0,1,2,…, (6.30)

где G -1 (Х k ) – матрица, обратная к матрице Гессе, вычисленная в точке поиска Х k (G (Х k ) × G -1 (Х k ) = I,

I = 0 1 … 0 - единичная матрица.

Рассмотрим пример поиска минимума для той же функции, что и в градиентном методе с постоянным шагом и в методе покоординатного спуска:

n = 2, X = (x 1 , x 2 ),  = 0.1,

Ф(x 1 , x 2 ) = (x 1 – 1) 2 + (x 2 – 2) 2  min , Х 0 =(0, 1).

Получим точку Х 1 :

X 1 = X 0 – G –1 (X 0)∙grad Ф(X 0),

где

grad Ф(X 0) = (2∙(x 1 0 –1)), 2∙(x 1 0 –1) = (–2, –2), то есть

или

x 1 1 = 0 – (1/2∙(–2) + 0∙(–2)) = 1,

x 2 1 = 1 – (0∙(–2) + 1/2∙(–2)) = 2,

X 1 = (1, 2).

Проверим выполнение условий прекращения поиска: первое условие не выполнено

Ф(X 1 )-Ф(X 0 ) = 0 - 2  = 2 >  = 0.1,

но справедливо

то есть все частные производные с точностью  можно считать равными нулю, точка минимума найдена: Х* = Х 1 = (1, 2). Траектория поиска совпадает с траекторией метода наискорейшего спуска (рис. 2.24).

Главным недостатком метода Ньютона являются затраты на вычисление обратного гессиана G -1 (Х k ) на каждой итерации метода.

В методе ДФП преодолены недостатки как метода наискорейшего спуска, так и метода Ньютона.

Достоинством данного метода является то, что он не требует вычисления обратного гессиана, а в качестве направления поиска в методе ДФП выбирается направление –Н k × grad Ф (Х k), где Н k - положительно определенная симметричная матрица, которая заново рассчитывается на каждой итерации (шаге метода поиска) и приближает обратный гессиан G -1 (Х k ) (Н k ® G -1 (Х k ) с увеличением k ).

Кроме того, метод ДФП при его применении для поиска экстремума функции n переменных сходится (то есть дает решение) не более чем за n итераций.

Вычислительная процедура метода ДФП включает следующие шаги.

Исходными данными являются требуемая точность e, начальная точка поиска Х 0 и начальная матрица Н 0 (обычно единичная матрица, Н 0 = I).

На k -ой итерации метода известны точка поиска Х k и матрица Н k (k = 0,1,…).

Обозначим направление поиска

d k = -Н k × grad Ф(Х k).

Находим оптимальную величину шага l k в направлении d k с помощью методов одномерной оптимизации (так же, как в методе наискорейшего спуска выбиралась величина в направлении веrтора антиградиента)

З. Обозначим v k = l k × d k и получим новую точку поиска Х k +1 = X k + v k .

4. Проверяем выполнение условия прекращения поиска.

Если ½v k ½£ e или ½grad Ф(Х k +1 ) ½£ e , то решение найдено Х * = Х k +1 . В противном случае продолжаем вычисления.

5. Обозначим u k = grad Ф(Х k +1) - grad Ф(Х k) и матрицу Н k +1 рассчитаем по формуле:

H k +1 = H k + A k + B k , (6.31)

где A k = v k . v k T / (v k T × u k ) , B k = - H k × u k . u k T . H k / (u k T × H k × u k ) .

A k и В k – это вспомогательные матрицы размера n х n (v k T соответствует вектору-строке, v k означает вектор-столбец, результатом умножения n -мерной строки на n -мерный столбец является скалярная величина (число), а умножение столбца на строку дает матрицу размера n x n ).

6. Увеличиваем номер итерации на единицу и переходим к пункту 2 данного алгоритма.

Метод ДФП – это мощная оптимизационная процедура, эффективная при оптимизации большинства функций. Для одномерной оптимизации величины шага в методе ДФП используют методы интерполяции.

Понятие SEO заключает в себя способы поднятия своего сайта в результатах поиска потенциальных посетителей. Это обычно поднимает трафик Вашего сайта.
В то время как интенсивная SEO оптимизация и продвижение сайта может вызвать затруднения с фирмой (или консультантом), который специализируется в этой области, есть несколько простых шагов, которые вы можете исполнить сами, чтобы увеличить ранжирование портала в поисковых системах. Все что от вас требуется - это немного усилий и переосмысление того, как вы относитесь к контенту (содержанию) сайта.

Изучите 10 основных принципов поисковой оптимизации сайтов

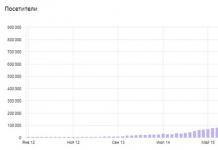
Монитор, за которым вы находитесь

Вы не будете знать, насколько продвижение сайта эффективно, если вы не контролируете позиции поиска. MarketingVox предлагает вам прослеживание за своим PR (Page Rank) с такими инструментами как Alexa и панель инструментов Google.
Также важно проверять, откуда пользователи приходят на ваш сайт, какие поисковые фразы используют. С этой задачей отлично справляется Яндекс Метрика.

Ключевые слова, ключевые слова, ключевые слова!

Вы должны осознано подбирать соответствующие ключевые слова для каждого аспекта Вашего сайта: title (заголовок), статья, URL и подпись к картинкам. Размышляйте при подборе ключевых словах следующим образом - будет ли полезна информация с моего сайта пользователю?
Тег title и заголовок страницы - два самых важных места, куда нужно вставить ключевые слова.
ПРЕДОСТЕРЕЖЕНИЕ: При использовании большого количества ключевых слов поисковые системы могут пометить вас как спамера и применить против вашего сайта санкции, вплоть до его исключения из поисковой системы. Придерживайтесь определённой стратегии при подборе ключевых слов.

Создайте карту сайта.

Добавление карты сайта - облегчает для поисковых систем поиск страниц сайта.
"Чем меньше кликов, необходимых для того, чтобы добраться до страницы Вашего веб-сайта, тем лучше", советует MarketingVox.

Благоприятные для поиска URLs адреса.

Сделайте URL более благоприятными для поисковой системы, используя в названии ключевые слова

Описание изображения.

Роботы могут искать только текст, а не текст в изображениях - именно поэтому Вы должны сделать слова связанные с Вашими изображениями максимально информативными.
Начните с названия изображения: добавление тега "ALT" позволяет Вам включать ключевые слова в описание каждого изображения веб-ресурса. Видимый текст вокруг ваших изображений важен для SEO.

Контент.

Ваш контент должно быть свежим, обновляться регулярно, что часто имеет решающее значение для увеличения трафика.
Лучшие сайты для пользователей и, следовательно, для поисковых систем постоянно обновляются полезной информацией.

Социальная медиа дистрибуция

Вы должны использовать различные тематические форумы, группы в социальных сетях и информационных порталах, близкие к теме вашего сайта, и писать туда анонсы с дальнейшей ссылкой на статью с вашего сайта.
Также вы должны поставить на свой сайт социальные кнопки и побуждать посетителей нажимать на них. Это всё стратегия экспоненциального размножения мест, где пользователи увидят ссылки на ваш ресурс.

Внешняя перелинковка

Легкий способ направить больше трафика на на свой web-ресур - развивать отношения с другими сайтами.
PC World предлагает, чтобы Вы лично договорились с веб-мастерами уважаемых сайтов, чтобы они разместили на своём сайте ссылку на нужный ресурс.
Удостоверьтесь, что у Вашего партнера есть хорошая веб-репутация, конечно. Не связываейтесь с сайтом, который обладает плохой репутацией, а то могут ухудшиться результаты поисковой оптимизации вашего сайта.