Distância de ponto a pontoé o comprimento do segmento que conecta esses pontos em uma determinada escala. Assim, quando se trata de medir distância, é preciso saber a escala (unidade de comprimento) em que serão feitas as medidas. Portanto, o problema de encontrar a distância de um ponto a outro é geralmente considerado em uma linha de coordenadas ou em um sistema de coordenadas cartesianas retangulares em um plano ou em um espaço tridimensional. Em outras palavras, na maioria das vezes é necessário calcular a distância entre os pontos usando suas coordenadas.

Neste artigo, lembraremos primeiro como é determinada a distância de um ponto a outro em uma linha de coordenadas. A seguir, obtemos fórmulas para calcular a distância entre dois pontos de um plano ou espaço de acordo com determinadas coordenadas. Concluindo, consideraremos detalhadamente as soluções para exemplos e problemas típicos.

Navegação na página.

A distância entre dois pontos em uma linha de coordenadas.

Vamos primeiro definir a notação. Denotaremos a distância do ponto A ao ponto B como.

Disto podemos concluir que a distância do ponto A com coordenada ao ponto B com coordenada é igual ao módulo da diferença de coordenadas, aquilo é, para qualquer localização de pontos na linha de coordenadas.

Distância de ponto a ponto em um plano, fórmula.

Obtemos uma fórmula para calcular a distância entre pontos e dada em um sistema de coordenadas cartesianas retangulares em um plano.

Dependendo da localização dos pontos A e B, as seguintes opções são possíveis.

Se os pontos A e B coincidem, então a distância entre eles é zero.

Se os pontos A e B estiverem em uma linha reta perpendicular ao eixo das abcissas, então os pontos coincidem e a distância é igual à distância . No parágrafo anterior, descobrimos que a distância entre dois pontos em uma reta coordenada é igual ao módulo da diferença entre suas coordenadas, portanto, . Por isso, .

Da mesma forma, se os pontos A e B estão em uma linha reta perpendicular ao eixo das ordenadas, então a distância do ponto A ao ponto B é encontrada como.

Neste caso, o triângulo ABC é retangular em construção, e E . Por teorema de Pitágoras podemos escrever a igualdade, de onde .

Vamos resumir todos os resultados obtidos: a distância de um ponto a um ponto em um plano é encontrada através das coordenadas dos pontos usando a fórmula .

A fórmula resultante para encontrar a distância entre os pontos pode ser usada quando os pontos A e B coincidem ou estão em uma linha reta perpendicular a um dos eixos coordenados. Na verdade, se A e B coincidem, então. Se os pontos A e B estiverem em uma linha reta perpendicular ao eixo do Boi, então. Se A e B estão em uma linha reta perpendicular ao eixo Oy, então .

Distância entre pontos no espaço, fórmula.

Vamos apresentar um sistema de coordenadas retangulares Oxyz no espaço. Vamos obter uma fórmula para encontrar a distância de um ponto ao ponto .

Em geral, os pontos A e B não estão num plano paralelo a um dos planos coordenados. Desenhemos através dos pontos A e B planos perpendiculares aos eixos coordenados Ox, Oy e Oz. Os pontos de intersecção desses planos com os eixos coordenados nos darão projeções dos pontos A e B sobre esses eixos. Denotamos as projeções .

A distância necessária entre os pontos A e B é a diagonal do paralelepípedo retangular mostrado na figura. Por construção, as dimensões deste paralelepípedo são iguais E . Num curso de geometria do ensino médio, foi comprovado que o quadrado da diagonal de um paralelepípedo é igual à soma dos quadrados de suas três dimensões, portanto, . Com base nas informações da primeira seção deste artigo, podemos escrever as seguintes igualdades, portanto,

de onde tiramos isso fórmula para encontrar a distância entre pontos no espaço .

Esta fórmula também é válida se os pontos A e B

• combinar;
• pertencem a um dos eixos coordenados ou a uma linha paralela a um dos eixos coordenados;
• pertencem a um dos planos coordenados ou a um plano paralelo a um dos planos coordenados.

Encontrando a distância de ponto a ponto, exemplos e soluções.

Assim, obtivemos fórmulas para encontrar a distância entre dois pontos em uma linha coordenada, plano e espaço tridimensional. É hora de procurar soluções para exemplos típicos.

O número de problemas em que o passo final é encontrar a distância entre dois pontos de acordo com as suas coordenadas é verdadeiramente enorme. Uma revisão completa de tais exemplos está além do escopo deste artigo. Aqui nos limitaremos a exemplos em que as coordenadas de dois pontos são conhecidas e é necessário calcular a distância entre eles.

Usando coordenadas, a localização de um objeto no globo é determinada. As coordenadas são indicadas por latitude e longitude. As latitudes são medidas a partir da linha do equador em ambos os lados. No Hemisfério Norte as latitudes são positivas, no Hemisfério Sul são negativas. A longitude é medida a partir do meridiano principal, leste ou oeste, respectivamente, sendo obtida a longitude leste ou oeste.

De acordo com a posição geralmente aceita, considera-se que o meridiano principal é aquele que passa pelo antigo Observatório de Greenwich, em Greenwich. As coordenadas geográficas do local podem ser obtidas por meio de um navegador GPS. Este dispositivo recebe sinais do sistema de posicionamento por satélite no sistema de coordenadas WGS-84, uniforme para todo o mundo.

Os modelos de navegador diferem em fabricante, funcionalidade e interface. Atualmente, navegadores GPS integrados também estão disponíveis em alguns modelos de celulares. Mas qualquer modelo pode registrar e salvar as coordenadas de um ponto.

Distância entre coordenadas GPS

Para resolver problemas práticos e teóricos em algumas indústrias, é necessário ser capaz de determinar as distâncias entre os pontos pelas suas coordenadas. Existem várias maneiras de fazer isso. A forma canônica de representação de coordenadas geográficas: graus, minutos, segundos.

Por exemplo, você pode determinar a distância entre as seguintes coordenadas: ponto nº 1 - latitude 55°45′07″ N, longitude 37°36′56″ E; ponto nº 2 - latitude 58°00′02″ N, longitude 102°39′42″ E.

A maneira mais fácil é usar uma calculadora para calcular o comprimento entre dois pontos. No mecanismo de busca do navegador, você deve definir os seguintes parâmetros de pesquisa: online - para calcular a distância entre duas coordenadas. Na calculadora online, os valores de latitude e longitude são inseridos nos campos de consulta da primeira e segunda coordenadas. Ao calcular, a calculadora online deu o resultado - 3.800.619 m.

O próximo método é mais trabalhoso, mas também mais visual. Você deve usar qualquer programa de mapeamento ou navegação disponível. Os programas nos quais você pode criar pontos usando coordenadas e medir distâncias entre eles incluem os seguintes aplicativos: BaseCamp (um análogo moderno do programa MapSource), Google Earth, SAS.Planet.

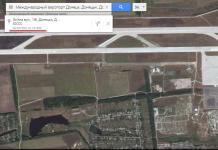
Todos os programas acima estão disponíveis para qualquer usuário da rede. Por exemplo, para calcular a distância entre duas coordenadas no Google Earth, você precisa criar dois rótulos indicando as coordenadas do primeiro ponto e do segundo ponto. Em seguida, usando a ferramenta “Régua”, é necessário conectar a primeira e a segunda marcas com uma linha, o programa exibirá automaticamente o resultado da medição e mostrará o caminho na imagem de satélite da Terra.

No caso do exemplo dado acima, o programa Google Earth retornou o resultado - o comprimento da distância entre o ponto nº 1 e o ponto nº 2 é 3.817.353 m.

Por que há um erro ao determinar a distância

Todos os cálculos da extensão entre as coordenadas são baseados no cálculo do comprimento do arco. O raio da Terra está envolvido no cálculo do comprimento do arco. Mas como a forma da Terra é próxima de um elipsóide achatado, o raio da Terra varia em certos pontos. Para calcular a distância entre as coordenadas, é tomado o valor médio do raio da Terra, o que dá um erro na medição. Quanto maior for a distância medida, maior será o erro.

Matemática

§2. Coordenadas de um ponto no plano

3. Distância entre dois pontos.

Você e eu agora podemos conversar sobre pontos na linguagem dos números. Por exemplo, não precisamos mais explicar: tomemos um ponto que está três unidades à direita do eixo e cinco unidades abaixo do eixo. Basta dizer simplesmente: entenda o que quero dizer.

Já dissemos que isso cria certas vantagens. Assim, podemos transmitir por telégrafo um desenho feito de pontos, comunicá-lo a um computador, que não entende nada de desenhos, mas entende bem os números.

No parágrafo anterior, definimos alguns conjuntos de pontos no plano utilizando relações entre números. Agora vamos tentar traduzir consistentemente outros conceitos e fatos geométricos para a linguagem dos números.

Começaremos com uma tarefa simples e comum.

Encontre a distância entre dois pontos no plano.

Solução:
Como sempre, assumimos que os pontos são dados pelas suas coordenadas, e então a nossa tarefa é encontrar uma regra pela qual possamos calcular a distância entre os pontos, conhecendo as suas coordenadas. Ao derivar esta regra, é claro, é permitido recorrer a um desenho, mas a regra em si não deve conter nenhuma referência ao desenho, mas apenas mostrar quais ações e em que ordem devem ser executadas nos números dados - as coordenadas dos pontos - para obter o número desejado - a distância entre os pontos.

Talvez alguns leitores achem essa abordagem para resolver o problema estranha e rebuscada. O que é mais simples, dirão, os pontos são dados, até por coordenadas. Desenhe esses pontos, pegue uma régua e meça a distância entre eles.

Este método às vezes não é tão ruim. No entanto, imagine novamente que você está lidando com um computador. Ela não tem régua e não desenha, mas consegue contar tão rápido que isso não é problema para ela. Observe que nosso problema está formulado de forma que a regra para calcular a distância entre dois pontos consiste em comandos que podem ser executados por uma máquina.

É melhor resolver primeiro o problema colocado para o caso especial quando um desses pontos está na origem das coordenadas. Comece com alguns exemplos numéricos: encontre a distância da origem dos pontos; E .

Observação. Use o teorema de Pitágoras.

Agora escreva uma fórmula geral para calcular a distância de um ponto à origem.

A distância de um ponto à origem é determinada pela fórmula:

Obviamente, a regra expressa por esta fórmula satisfaz as condições acima expostas. Em particular, pode ser usado em cálculos em máquinas que podem multiplicar números, somá-los e extrair raízes quadradas.

Agora vamos resolver o problema geral

Dados dois pontos de um plano, encontre a distância entre eles.

Solução:
Denotemos por , , , as projeções dos pontos e nos eixos coordenados.

Vamos denotar o ponto de intersecção das retas com a letra . De um triângulo retângulo usando o teorema de Pitágoras obtemos:

Mas o comprimento do segmento é igual ao comprimento do segmento. Os pontos e , estão no eixo e possuem coordenadas e , respectivamente. De acordo com a fórmula obtida no parágrafo 3 do parágrafo 2, a distância entre eles é igual a .

Argumentando de forma semelhante, descobrimos que o comprimento do segmento é igual a. Substituindo os valores encontrados e na fórmula obtemos.

Calcular distâncias entre pontos com base em suas coordenadas em um plano é elementar; na superfície da Terra é um pouco mais complicado: consideraremos medir a distância e o azimute inicial entre pontos sem transformações de projeção. Primeiro, vamos entender a terminologia.

Introdução

Grande comprimento do arco circular– a distância mais curta entre quaisquer dois pontos localizados na superfície de uma esfera, medida ao longo da linha que conecta esses dois pontos (tal linha é chamada de ortodromia) e passando ao longo da superfície da esfera ou outra superfície de rotação. A geometria esférica é diferente da geometria euclidiana normal e as equações de distância também assumem uma forma diferente. Na geometria euclidiana, a distância mais curta entre dois pontos é uma linha reta. Numa esfera não existem linhas retas. Essas linhas na esfera fazem parte de círculos máximos - círculos cujos centros coincidem com o centro da esfera. Azimute inicial- azimute, tomando-se que ao começar a se mover do ponto A, seguindo um círculo máximo pela distância mais curta até o ponto B, o ponto final será o ponto B. Ao se mover do ponto A ao ponto B ao longo da linha do grande círculo, o azimute de a posição atual até o ponto final B é constante e está mudando. O azimute inicial é diferente de um constante, após o qual o azimute do ponto atual ao ponto final não muda, mas a rota seguida não é a distância mais curta entre dois pontos.

Através de quaisquer dois pontos na superfície de uma esfera, se não forem diretamente opostos um ao outro (ou seja, não forem antípodas), um único grande círculo pode ser desenhado. Dois pontos dividem um grande círculo em dois arcos. O comprimento de um arco curto é a distância mais curta entre dois pontos. Um número infinito de círculos grandes pode ser desenhado entre dois pontos antípodas, mas a distância entre eles será a mesma em qualquer círculo e igual à metade da circunferência do círculo, ou π*R, onde R é o raio da esfera.

Em um plano (em um sistema de coordenadas retangulares), grandes círculos e seus fragmentos, como mencionado acima, representam arcos em todas as projeções, exceto na gnomônica, onde grandes círculos são linhas retas. Na prática, isso significa que os aviões e outros transportes aéreos sempre utilizam a rota da distância mínima entre os pontos para economizar combustível, ou seja, o vôo é realizado ao longo de uma distância de grande círculo, no avião parece um arco.

A forma da Terra pode ser descrita como uma esfera, portanto, as equações de distância do grande círculo são importantes para calcular a distância mais curta entre pontos na superfície da Terra e são frequentemente usadas na navegação. Calcular a distância por este método é mais eficiente e em muitos casos mais preciso do que calculá-la para coordenadas projetadas (em sistemas de coordenadas retangulares), pois, em primeiro lugar, não requer a conversão de coordenadas geográficas para um sistema de coordenadas retangulares (realizar transformações de projeção) e , em segundo lugar, muitas projeções, se selecionadas incorretamente, podem levar a distorções significativas de comprimento devido à natureza das distorções de projeção. Sabe-se que não se trata de uma esfera, mas sim de um elipsóide que descreve com maior precisão o formato da Terra, porém, este artigo aborda o cálculo de distâncias especificamente sobre uma esfera; para os cálculos utiliza-se uma esfera com raio de 6.372.795 metros , o que pode levar a um erro no cálculo de distâncias da ordem de 0,5%.

Fórmulas

Existem três maneiras de calcular a distância esférica do grande círculo. 1. Teorema do cosseno esférico No caso de distâncias pequenas e profundidade de cálculo pequena (número de casas decimais), o uso da fórmula pode levar a erros de arredondamento significativos. φ1, λ1; φ2, λ2 - latitude e longitude de dois pontos em radianos Δλ - diferença de coordenadas em longitude Δδ - diferença angular Δδ = arccos (sen φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) Para converter a distância angular em métrica, você precisa multiplique a diferença angular pelo raio da Terra (6372795 metros), as unidades da distância final serão iguais às unidades em que o raio é expresso (neste caso, metros). 2. Fórmula de Haversina Usado para evitar problemas com distâncias curtas. 3. Modificação para os antípodas A fórmula anterior também está sujeita ao problema dos pontos antípodas, para resolvê-lo utiliza-se a seguinte modificação.

Minha implementação em PHP

// Raio da Terra define("EARTH_RADIUS", 6372795); /* * Distância entre dois pontos * $φA, $λA - latitude, longitude do 1º ponto, * $φB, $λB - latitude, longitude do 2º ponto * Escrito com base em http://gis-lab.info/ qa/great-circles.html *Mikhail Kobzarev< >* */ function calculaTheDistance ($φA, $λA, $φB, $λB) ( // converte coordenadas em radianos $lat1 = $φA * M_PI / 180; $lat2 = $φB * M_PI / 180; $long1 = $λA * M_PI / 180; $long2 = $λB * M_PI / 180; // cossenos e senos de diferenças de latitudes e longitudes $cl1 = cos($lat1); $cl2 = cos($lat2); $sl1 = sin($lat1) ) ; $sl2 = sin($lat2); $delta = $long2 - $long1; $cdelta = cos($delta); $sdelta = sin($delta); // cálculos do comprimento do círculo máximo $y = sqrt(pow ( $cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2)); $x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta; / / $ad = atan2($y, $x); $dist = $ad * EARTH_RADIUS; return $dist; ) Exemplo de chamada de função: $lat1 = 77.1539; $longo1 = -139,398; $lat2 = -77,1804; $longo2 = -139,55; echo calculaTheDistance($lat1, $long1, $lat2, $long2) . "metros"; // Retorna "17166029 metros"

Artigo retirado do site